Recently, I’ve been studying for my PhD Qualifying exams (update: Passed!). Which means my days have tended to look like this:

All day, every day

My research relates to quantum computers. Quantum computers will be transformative for many areas, including:

Computer Security

Quantum computers would massively speed up our ability to factor large numbers into their constituent prime numbers (for instance, 100 into 5x5x2x2).

This seems trivial. But it would actually break much of computer security. Large numbers are jerks, and they have decided to make it almost impossible to factor them in any reasonable timeframe.

Public-key cryptography often relies on this fact for ensuring computer security. These jerk-ish large numbers act like the bodyguards for much of our secure information on the internet. But a large-scale quantum computer could actually factor these large numbers quickly. One person with a large-scale quantum computer could potentially acquire government secrets, steal money from strangers’ bank accounts, and read their encrypted emails.

The good news is that the government is aware of this problem, and they’re already working to mitigate it. The NSA is advising companies building new systems to use algorithms safe against quantum computers.

The bad news is that we don’t have any algorithms that we know are safe, only ones that we think are safe. So the NSA is telling companies to use algorithms “believed to be safe.”

Yikes. Hopefully, everything works out okay.

Computational Chemistry, Biology, Nanotechnology, etc

This is the area I’m most excited about.

Currently, scientific simulations face a major tradeoff:

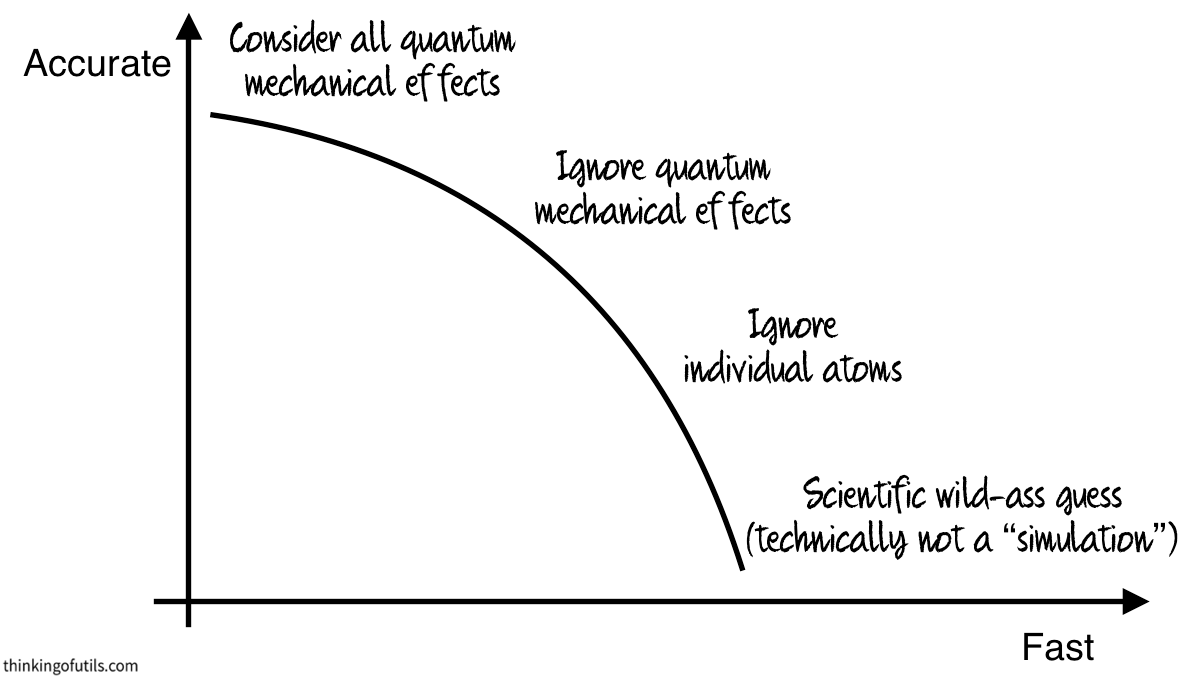
The most accurate techniques for simulating materials involve simulating all atoms and electrons according to quantum mechanical rules. Unfortunately, this is impractical for all but the smallest systems (meaning a few atoms). This is because the time it takes to run these simulations gets exponentially larger as the number of atoms in the simulation increases.

A quantum computer could simulate many of these physical processes in a time that does not increase exponentially with the number of atoms.

And this means quantum computers would allow for much more extravagant simulations of chemistry, biology, and materials science.

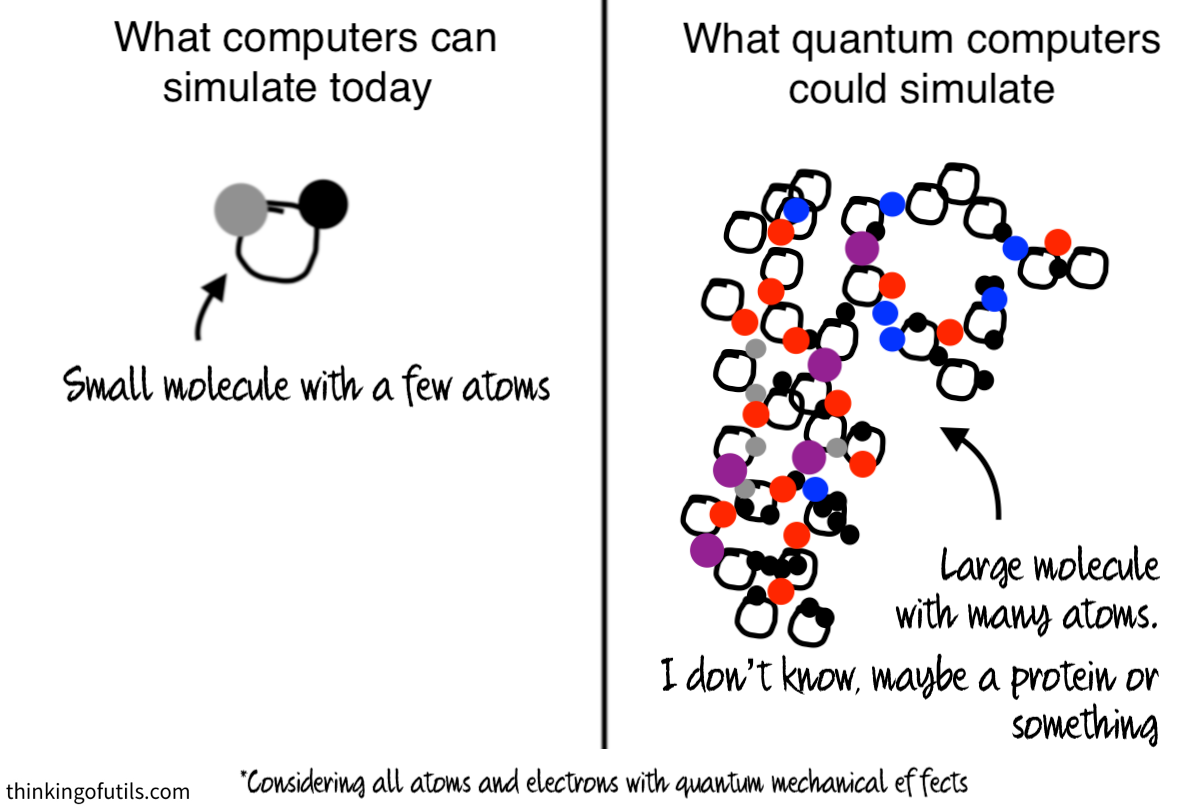
In addition to helping us understand these fields better, quantum computers could also help us engineer our own large molecules with desired properties. Chemical engineering, bioengineering, and materials engineering could advance at a higher rate.

Of particular interest to humans like us, quantum computers could have major ramifications for medicine. Since most diseases and aging occur on the subcellular scale, the ability to understand this scale with accurate simulations – and to manipulate matter on this scale with specially designed molecules – could enable us to create cures we can only dream of today.

Unfortunately, not a lot has been written about quantum computers in an easy to understand manner. In the rest of this post, I’m going to attempt to clear up some of the confusion on the topic.

Okay, let’s get started.

The best starting place to understand quantum computers is to first get some baseline understanding of classical computers (“classical computers” is a fancy way of saying “computers that are not quantum computers,” or what normal people simply call “computers”).

 

Classical Computers

Computers are awesome. ‘Nuff said. Despite being quite versatile, they’re actually pretty simple.

Google Dictionary tells me that the definition of a computer is “an electronic device for storing and processing data, typically in binary form, according to instructions given to it in a variable program.”

Google also tells me that “ultraportable” and “puter” are synonyms for computer. I’ve literally never heard either of those words before, so I think Google might just be messing with me.

The operative words in the definition are storing and processing. Computers store and process information.

Bits: storing information

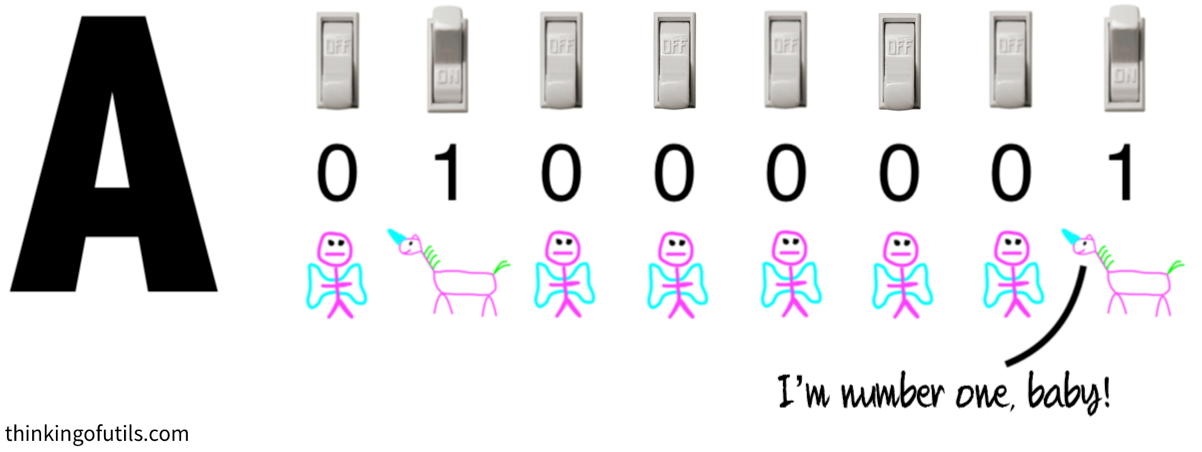
In classical computers, information is stored in “bits,” with each bit representing a 0 or a 1.

What this means is that information is stored as if by a bunch of switches that can either be off or on. By convention, computer scientists have chosen to call these “0” and “1” for off and on. They just as easily could have called them apples and oranges, or fairies and unicorns.

Had they chosen the latter, a sequence of information in a computer wouldn’t read “00110101” but instead “fairy-fairy-unicorn-unicorn-fairy-unicorn-fairy-unicorn” and everything else would work exactly as it does today.

Since most information is more complicated than can be expressed with a single bit, longer sequences are used. For instance, “A” can be encoded by “01000001,” “B” by “01000010,” and so on.

Logic Gates: processing information

Of course, computers do much more than just store information – they also process it in desired ways, using “logic gates.”

A logic gate takes two bits of information as input and outputs one bit. You can think of a logic gate as a magical wizard that takes some combination of unicorns and fairies and combines each pair into either one unicorn or one fairy, according to his perverse wizarding rules.

There are many different types of logic gates. We’ll examine AND gates and OR gates to get a sense for how logic gates work.

The AND gate will output a “1” if both of the input bits are “1,” but will output a “0” otherwise:

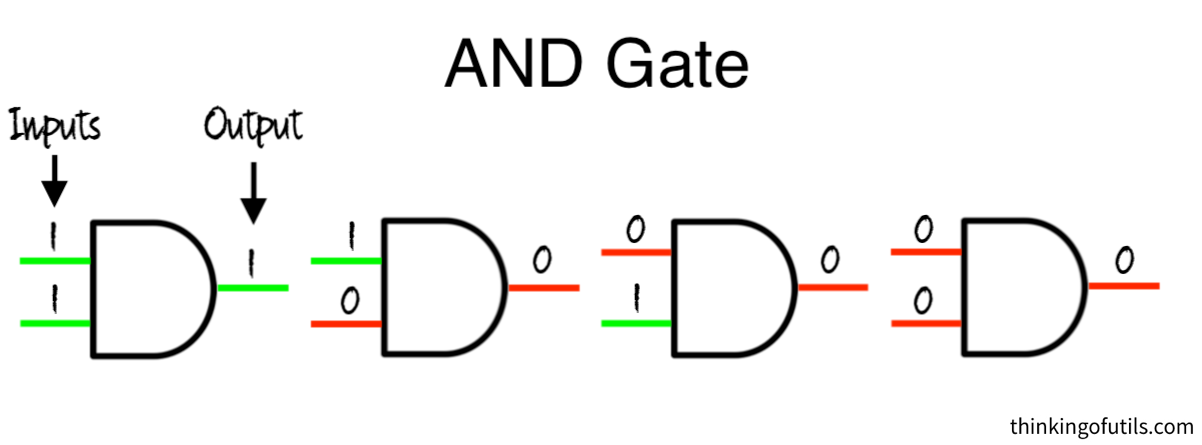
An AND gate is similar to a hallway with 2 doors – both doors need to be unlocked for you to be able to pass through.

An OR gate outputs 1 if at least one of the bits is 1 (and outputs a 0 otherwise). This can be thought of as a house with a front door and a back door. Only one of the doors needs to be unlocked for you to get into the house.

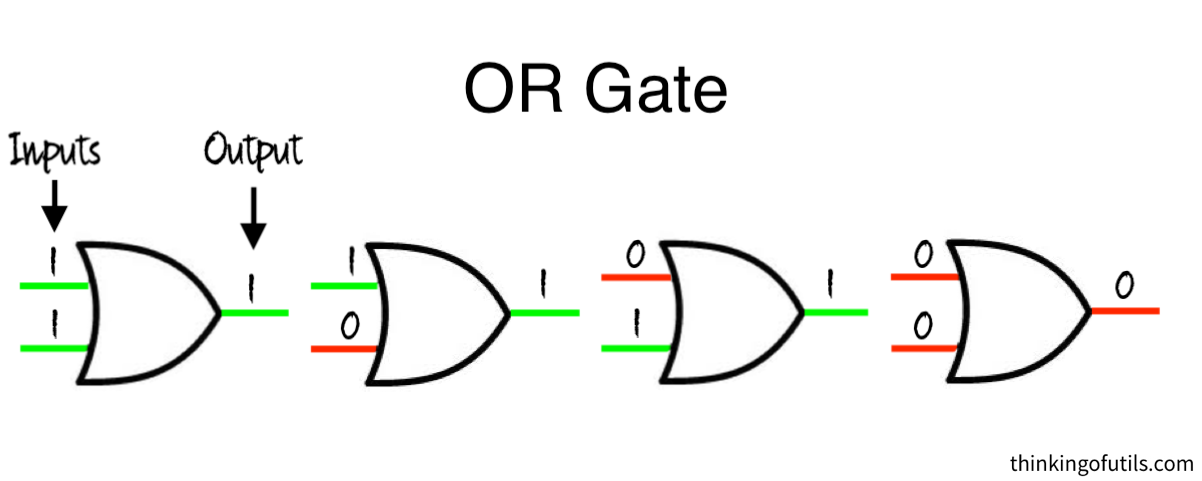
Other logic gates exist such that other combinations of input bits lead to specific output bits.

Computer scientists have created computer languages by storing information that instructs which logic gates should handle which further information under which conditions, and computer programs are created using these computer languages. Input to the computer, such as by the mouse and keyboard, gets converted into information that is then processed by logic gates.

And that’s more or less all there is to classical computers. Each computer has a very large (and growing ever year!) number of magical wizards that continuously combine fairies and unicorns such that certain combinations of fairies and unicorns are produced – some of which inform other wizards as what rules to follow and some of which correspond to outputs we care about deeply like an answer to a math problem or the audio of a Justin Bieber song.

Pretty simple, right? Ok, now onto the fun stuff!

Quantum Computers

Quantum computers work by exploiting bizarre effects in quantum mechanics – the physics on the atomic and subatomic level. In quantum mechanics, things are really weird. Individual particles can be in multiple locations at the same time, certain properties of particles are fundamentally unknowable, and so on.

[Note: quantum mechanics does NOT mean that consciousness existed before the Big Bang, that there is no such thing as absolute truth in our human-scale world, or any other woo-woo pseudoscientific or postmodernistic belief. Yes, stuff is really weird on the quantum scale. Quantum mechanics has been verified extensively – both mathematically and experimentally. Don’t use the weirdness of quantum mechanics as cover to make silly claims, and the only people you should listen to about the implications of quantum mechanics are people who know what they’re talking about – you know, actual scientists and engineers – not Deepak Chopra.]

Qubit: a quantum bit

In quantum computers, information isn’t stored in bits, it’s stored in qubits. A qubit is somewhat similar to a bit. But instead of information being stored as EITHER a 0 or a 1, it’s stored as BOTH 0 and 1, AT THE SAME TIME – due to something called superposition.

Superposition is one of those weird quantum mechanical concepts that doesn’t parallel anything we have on the human-scale. It can be understood in terms of something known as electron spin, though it also applies to many other properties.

All electrons have a quantum mechanical property known as “spin,” and the possible values for the spin are “up” and “down.” So does that mean that, for a given electron, the spin is either up or down? No, not quite. Electrons are shifty little rascals, so they’ve decided to make the situation a lot more complicated.

There are many experiments that can be performed to observe an electron’s spin. But before it’s observed, the spin will be BOTH up and down. We can say that it is some percent up and some percent down. Note that it’s not part way between up and down – it is quite literally both up and down.

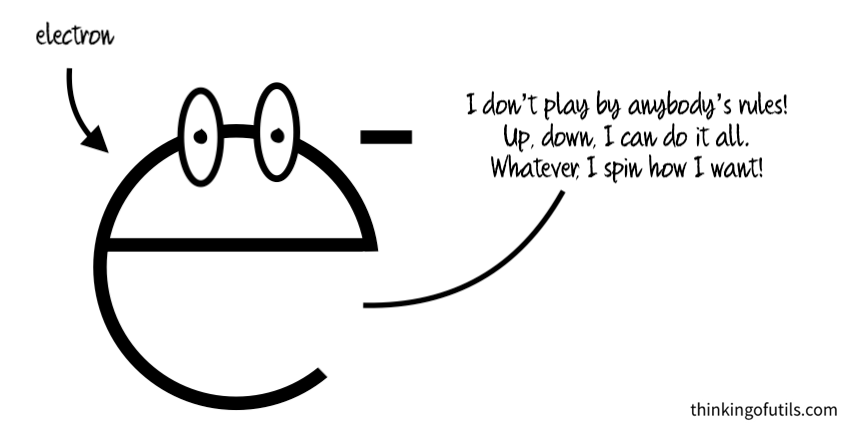
Now, when we observe the electron’s spin, it will appear either up or down, each with the probability corresponding to what percent up/ down it was before observing it. After being observed, the electron will stop acting so smug and will just keep whatever spin it was observed at.

If this doesn’t make sense intuitively, recognize that the math works and it’s very well established experimentally. You’re just going to have to accept it. And if you feel like this DOES make sense intuitively, then you’re just wrong. Go back and read it again until it stops making complete sense, since you’re clearly missing something.

And qubits use this same principle of superposition.

A qubit doesn’t just have two options like a bit – it has an infinite number of options, as it could be any percent 0 (and 100% minus that percent 1). You can think of a qubit as a magic creature that is x% unicorn and y% = 100% – x% fairy, but when you look at it, it transforms either into just a fairy or a unicorn. We’ll call that a “fairicorn.”

In reality, both x and y are made up of two separate numbers: x = a² + b², and y = c² + d². So we have even more numbers that we can vary, and we can store even more information. [Clarification for the mathematically inclined: the “weight” of 0 and 1 in a qubit – or of states in a quantum superposition more generally – are described as complex numbers. Here, a and b (or c and d) correspond to the real and imaginary parts of these complex numbers.]

But what if you have multiple qubits?

The first idea most people have is that each qubits would act independently. The first qubit might be x% “0” and y% “1.” The second qubit might be p% “0” and q% “1.” And so on.

That is WRONG.

Turns out, the fairicorns can actually talk with each other and can coordinate, in a process called quantum entanglement.

Quantum Entanglement is another one of those weird quantum mechanical concepts, which basically means that the quantum mechanical states of different parts of a system can be correlated. To demonstrate, imagine if we have two electrons that are each in a superposition of up and down. If they’re entangled, then we could know that they both have the same spin (or that they have opposite spins, depending on how they’re entangled). If we measure the first one and find that it’s up, we’d know the second one was up for sure (or down for sure if they were entangled to have opposite spins).

Again, this is very well established mathematically and experimentally. Scientists disagree about many things. But we don’t disagree about whether quantum superposition and quantum entanglement are real phenomena (at least not anymore).

So here’s what we’re left with. A system with two qubits will be x% “00,” y% “01,” p% “10,” and q% “11.” The only constraint is that x% + y% + p% + q% = 100%. And again, each of these numbers (x, y, p, and q) are actually made up of two separate numbers.

We can store MUCH more information in a certain amount of qubits than in the same amount of bits.

But when we observe the qubits (i.e. when a quantum computer outputs any information), we’ll just see a sequence of bits. The fairicorns all turn into fairies and unicorns when we look at them. The extra information that qubits store can be useful for information processing, but not for output.

The real power of quantum computing comes from how the information is processed.

Quantum Logic Gates

Just like in classical computers, quantum computers have logic gates – though they’re a bit more complicated. Here, the wizards will look at a group of fairicorns and manipulate them into a similarly sized group of different fairicorns. They still use a set of rules for the manipulation, but typically the resulting fairicorns will be a different percent fairy and unicorn from before.

Most quantum logic gates act on one or two qubits at a time.

[If you’re skimming this piece, stop to actually read this next bit. It explains the heart of why quantum computers would be so powerful.]

Let’s consider a single qubit. It’s x% “0”, where x = a² + b², and it’s y% “1,” where y = c² + d².

A quantum logic gate will take a, b, c, and d as input, and output new values for a, b, c, and d. This will typically change the values of x and y as well.

Each of the four variable (a, b, c, and d) is updated based on a mathematical equation specific to the logic gate. Like with classical logic gates, there are many different types of quantum logic gates. Again, we’ll examine only a couple – the “Pauli-Y gate” and the “Hadamard gate.”

The Pauli-Y gate will shuffle around the values of a, b, c, and d. The new value of a is the old value of d, the new value of b is the negative of the old value of c, the new value of c is the negative of the old value of b, and the new value of d is the old value of a.

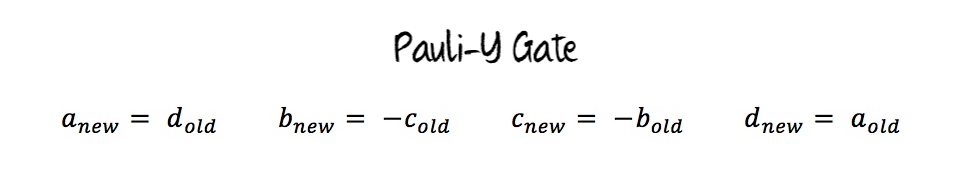
The Hadamard gate is a bit more complicated. Here, the new value of a is the sum of the old values of a and c, divided by the square root of 2. The new values of b, c, and d are similarly the sums (or in the cases of c and d, the differences) of two of the old values, divided by the square root of 2.

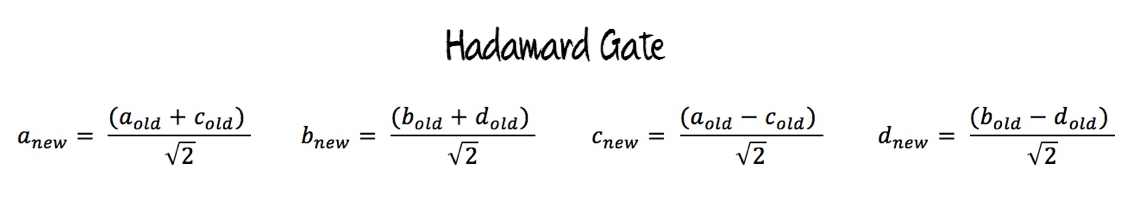
Quantum logic gates that affects two qubits follow similar principles to those that affect one qubit. Here, we have x% “00,” y% “01,” p% “10,” and q% “11.” Since each of those four parameters is actually composed of two separate numbers, we have eight variables in total. The logic gate will affect all of the eight variables, with each potentially affected by all eight original values.

Implications

People often say quantum computers “let you instantly solve problems by testing all answers at the same time.” As UT Austin computer science professor Scott Aaronson likes to say on his blog Shtetl-Optimized: that’s not true.

What quantum computers do is let you perform complicated operations that affect many pieces of information simultaneously, with each operation based on many pieces of information.

This doesn’t speed up every problem. There are many problems that would be no easier to solve on a quantum computer than a classical computer. But certain problems can be solved in WAY fewer steps – and thus MUCH faster.

Let’s dig down on this point a little deeper to understand how truly powerful quantum computers could be.

Consider the equation y = 2^x. This is known as an “exponential.” Increasing x by 1 (whether from 1 to 2, or from 145,346 to 145,347) causes the value of y to double. Exponentials are VERY VERY unintuitive to most people – even most techie people.

Now let’s consider another equation: y = x². This is known as a “polynomial.” At first glance, it looks pretty similar to an exponential. But when you get to large numbers, exponentials are ALWAYS much larger than polynomials.

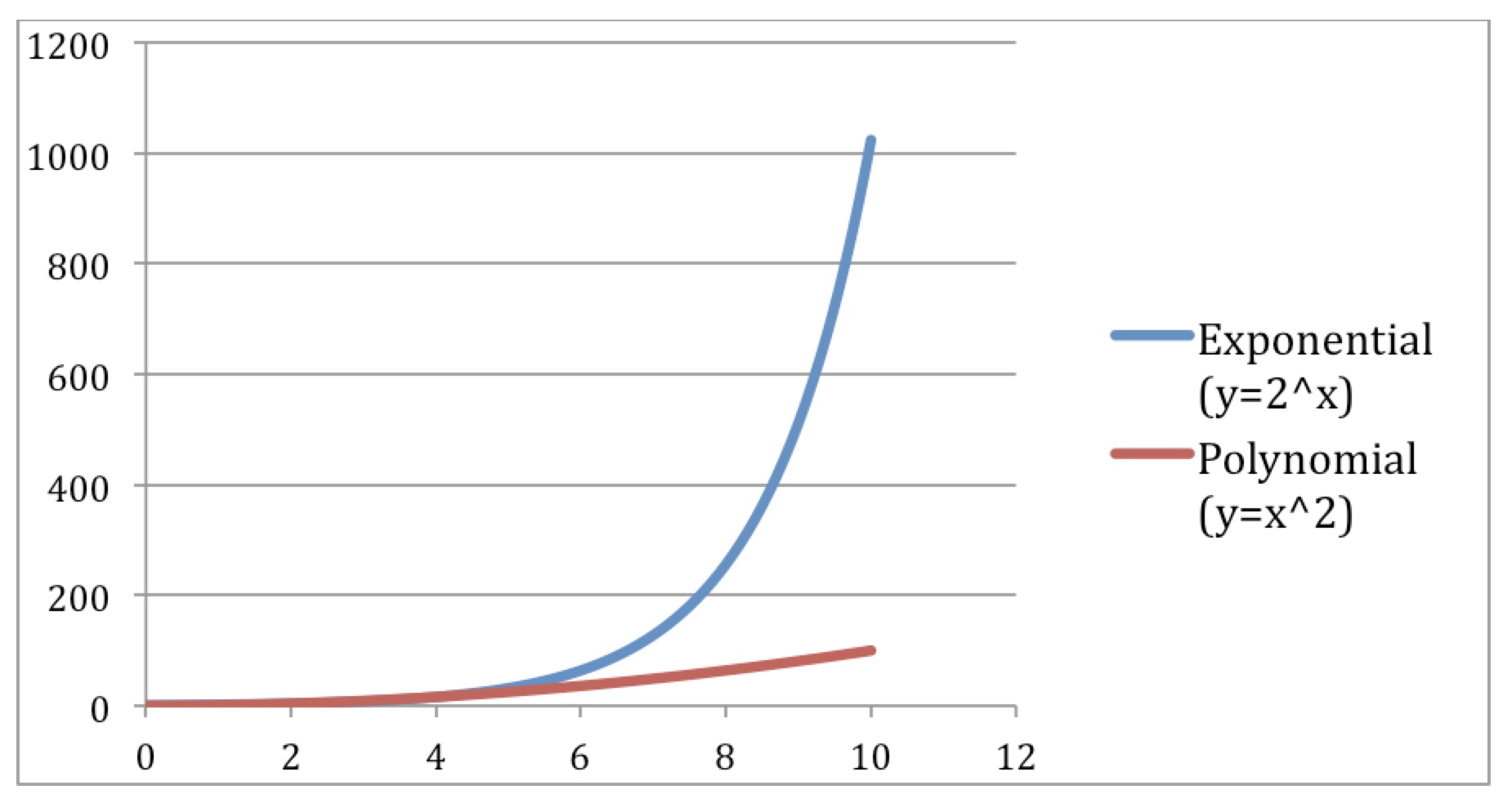
Great. Why do we care?

Because this is the difference in power between classical computers and quantum computers on some problems.

What do you think would happen if you were to take a problem and make it larger? For instance, what if you ran a chemical simulation with more atoms, or searched a database with more entries?

For most problems, the time to completion would increase. But it wouldn’t necessarily increase linearly. That would depend on the problem.

There are some problems that, as the size of the problem increases, the time to completion increases exponentially on a classical computer, but only increases polynomially on a quantum computer.

The time to complete the problem becomes absurdly high on a classical computer, but can be solved in a reasonable time on a quantum computer.

With 50-ish qubits, a quantum computer would likely be able to solve some problems on par with our fastest supercomputers. Quantum computers with greater capabilities than this are said to have achieved “quantum supremacy.”

With 500 qubits, a quantum computer would be able to solve some problems better than the best theoretical classical computer ever could.

That is to say, if all the mass in the observable universe was turned into an incredibly efficient classical computer, and that classical computer was allowed to run for many multiples of the age of the universe, it would not come close to solving certain problems that a 500-qubit quantum computer could solve in under a minute.

That’s the difference between polynomials and exponentials.

And we’d see that difference on some problems that we care about – such as certain atom-based science simulations (alluded to toward the beginning of this piece).

People often throw around the word “exponential” as if it just meant “a really really large amount,” or “related to really really cool technology.” One smart individual once mentioned to me that my own field of nanotechnology is “an exponential field” (whatever the hell that means).

Unlike a lot of misuses of “exponential,” quantum computing really would allow for exponentially more capabilities than what’s currently available.

Decoherence: Why large scale Quantum Computers have not been built yet

So now you’re probably wondering why quantum computers have only kinda/sorta/not-really been built. Turns out, quantum effects are really hard to control. When a system of qubits is not perfectly isolated, the information in the qubits is gradually lost to the environment. This is known as quantum decoherence. Basically, the fairicorns become confused. They think they’re supposed to be a different percent fairy/ unicorn than what they’re actually supposed to be.

And this is a REALLY HARD problem to solve.

There have been many proposals and proofs of concept for quantum computers, but all of them suffer from decoherence. Temperatures typically need to be decreased to near absolute zero, and even then, decoherence generally occurs within nanoseconds to seconds.

Until a few years ago, almost all progress in quantum computing came from academia. More recently, the private sector has started to address the technology as well.

Google, IBM, Intel, Microsoft, and Rigetti Computing are all hard at work trying to fix the issues related to decoherence. (D-Wave is also working on a “quantum annealer” – which is somewhat like a quantum computer and allows for many more qubits, but suffers from other problems and even in theory could only ever solve a small subset of problems that quantum computers could solve.)

Intel has recently started delivering 17-qubit quantum computing chips, and IBM has announced a 50-qubit quantum computer that can last for 90 microseconds.

It’s looking like some combination of Google/IBM/Intel/Microsoft/Rigetti might be within a few years of breaking the 50-ish qubit threshold of better-than-our-best-classical-supercomputers mark of quantum supremacy.

But due to decoherence, it will be tough to get the few hundred qubits necessary for better-than-all-matter-in-observable-universe-converted-to-efficient-classical-computer-running-for-lifetimes-of-universe capabilities that are the true promise of quantum computing.

My research is on a form of quantum computing known as topological quantum computing, which would be particularly stable against decoherence. Topological quantum computing relies on exotic behavior from particle interactions that have yet to be observed experimentally.

And I’ll probably write a post about that… after my dissertation.

If you build it, they will come

“I think there is a world market for maybe five computers”

–common misquote from Thomas Watson, Chairman and CEO of IBM, 1943

It’s a good quote, even though he never actually said that, nor (to my knowledge) did he ever imply anything to that effect.

But there were many people who said things along those lines. The truth is, quantum computers might be WAY bigger than anything we can imagine. We can think of a few very impactful uses now (see top of this post). Once quantum computers exist, however, resources will pour into finding profitable uses.

In 1943, no one thought we’d all have personal computers in our pockets, connected to a wireless database of all of human knowledge, and then we’d use this almost infinite database of knowledge to watch videos of cats being cats and to find strangers to date and/ or bum rides off of.

The implications of quantum computers will likely be far beyond anything I can imagine right now. For instance:

Quantum online dating – meet people that you’re both dating and not dating, AT THE SAME TIME. Actually, that just sounds like regular online dating…

Quantum cat videos – watch cute videos of cats that are both… you know what, we won’t even go there.

Hmm, maybe there aren’t that many applications for quantum computers after all.

—

Enjoy this post? 

Join the Thinking of Utils newsletter and get new posts emailed directly to you:

Facebook Comments

comments